Commutative Property Of Matrix Multiplication

Matrix Multiplication Divers (page 2 of 3)

Simply as with calculation matrices, the sizes of the matrices matter when we are multiplying. For matrix multiplication to piece of work, the columns of the second matrix have to take the same number of entries as practice the rows of the get-go matrix.

AB =

[[ 1 0 -2 ][ 0 3 -1 ]] � [[ 0 3 ][ -2 -1 ][ 0 4 ]]

If, using the above matrices, B had had only 2 rows, its columns would have been too brusk to multiply against the rows of A . Then " AB " would not accept existed; the product would have been "undefined". Likewise, if B had had, say, four rows, or alternatively if A had had 2 or 4 columns, so AB would non have existed, considering A and B would non have been the right sizes.

In other words, for AB to be (that is, for the very process of matrix multiplication to be able to function sensibly), A must have the aforementioned number of columns every bit B has rows; looking at the matrices, the rows of A must exist the same length as the columns of B .

You can use this fact to check speedily whether a given multiplication is divers. Write the product in terms of the matrix dimensions. In the case of the in a higher place trouble, A is ii�3 and B is three�2 , so AB is (two�3)(3�ii) . The middle values match:

...so the multiplication is defined. Past the way, you lot will retrieve that AB , the product matrix, was 2�two . You can also see this on the dimensions:

Using this, you can see that BA must be a unlike matrix from AB , because:

(3�2)(2�3): the inner dimensions match; the outer dimensions indicate a 3�3 product

The product BA is defined (that is, we tin can do the multiplication), simply the product, when the matrices are multiplied in this order, will exist 3�three , not 2�2 . In particular, matrix multiplication is not " commutative "; you cannot switch the club of the factors and expect to stop up with the same result. (Y'all should expect to come across a "concept" question relating to this fact on your next test.)

Given the following matrices, find the production BA .

A = [[ 1 0 -2 ][ 0 3 -1 ]] , B = [[ 0 3 ][ -2 -1 ][ 0 4 ]]

The multiplication works the same mode every bit the previous problem, going beyond the rows and downwards the columns. I won't endeavour cartoon my hands again, simply you can run across the computations in the colors below: Copyright � Elizabeth Stapel 2003-2011 All Rights Reserved

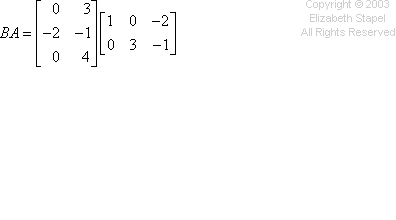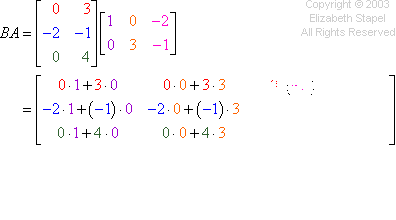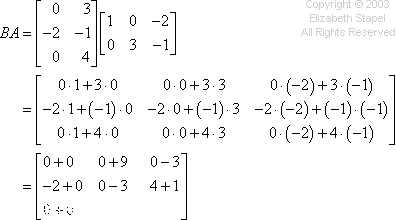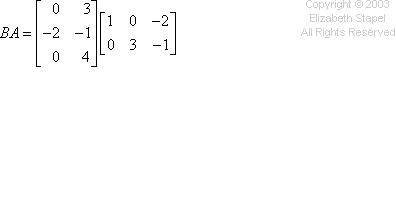
Demonstrates, using color, the process of matrix multiplication.

And then the respond is:

BA = [[ 0 9 3 ][ -2 -3 5 ][ 0 12 -4 ]]

Matrix multiplication is probably the first time that the Commutative Property has e'er been an effect. Remember when they made a big deal, back in eye school or before, nigh how " ab = ba " or " v�half dozen = six�v "? That "rule" probably seemed fairly stupid at the time, because you already knew that club didn't matter in multiplication. Introducing you to those rules back and so was probably kind of pointless, since order didn't matter for annihilation you were multiplying so. Well, now the Law of Commutativity does affair, because gild does matter for matrix multiplication. Always keep in mind that, for matrices, AB nigh certainly does not equal BA .